Table of Links
3. The GAR(1) Model
3.1. Model and Stationary Solution
4. Estimation of model parameters and 4.1. Fréchet mean
5. Testing for the absence of serial dependence
6.1. R with multiplicative noise
6.2. Univariate distributions with a density
Appendix A. General results in Hadamard spaces
7. Application
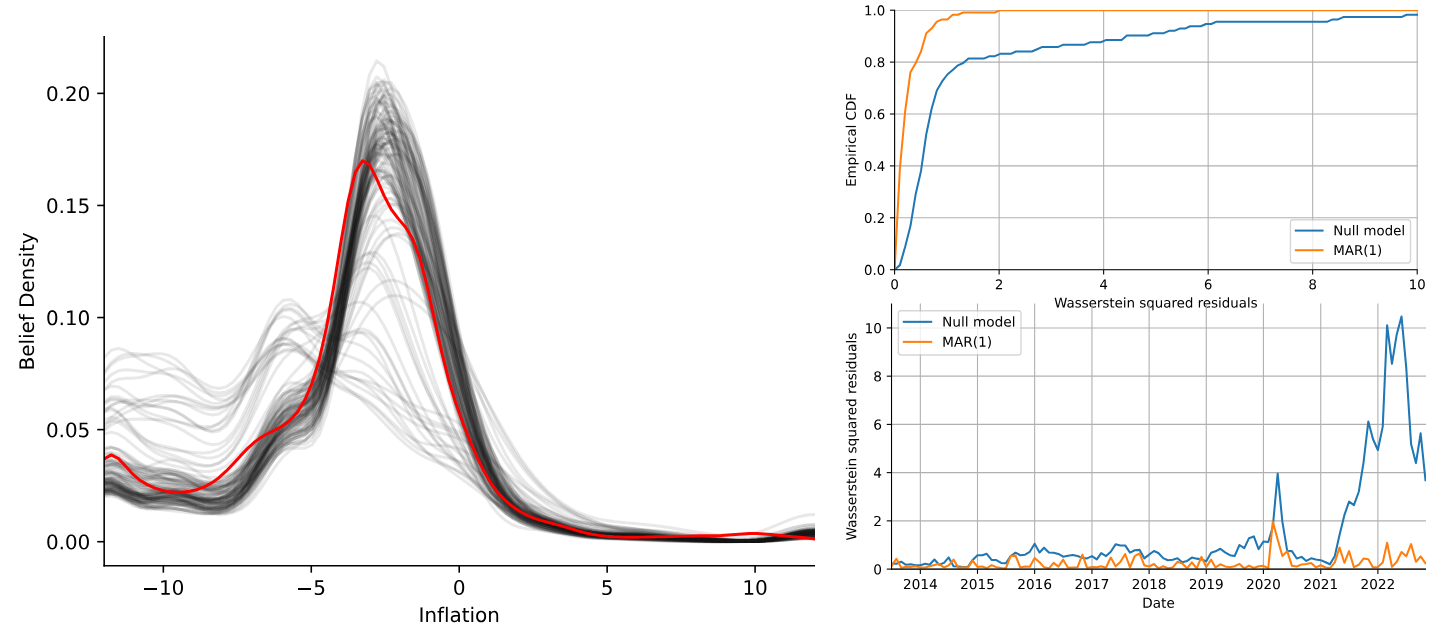
Analyzing consumer inflation expectations brings insights into how everyday perceptions shape broader economic trends (Dietrich et al., 2022; Meeks and Monti, 2023). The Survey of Consumer Expectations (SCE) is a monthly survey maintained by the Federal Reserve Bank of New York collecting information on households’ expectations on a broad variety of economic topics between June 2013 and November 2022, see Armantier et al. (2017). We focus our attention on the inflation expectation question, in which each consumer is asked to provide a distribution representing their belief for the 12-months ahead inflation. The survey respondents are presented with pre-defined bins over which they can distribute percentage points, defining a histogram of their beliefs. Each month, an average of approximately 1300 response histograms are available, which we aggregate by first taking the individual’s median belief and approximating the median belief density via kernel density estimator with a Gaussian kernel and using Scott’s rule (Scott, 1992) for the choice of the bandwidth, resulting in a time-series of T = 114 elements in D([−12, 12]) displayed in the left panel of Figure 6.

8. Acknowledgement
This work has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sk lodowska-Curie grant agreement No 956107, ”Economic Policy in Complex Environments (EPOC)”.
Appendix A. General results in Hadamard spaces
We start by stating results available in Hadamard spaces that will be used in the rest of the Appendix.

Appendix B. Proofs
Consistency of the mean estimator


Plugin this bound in the infinite sum, this gives

Using this bound in the sum gives
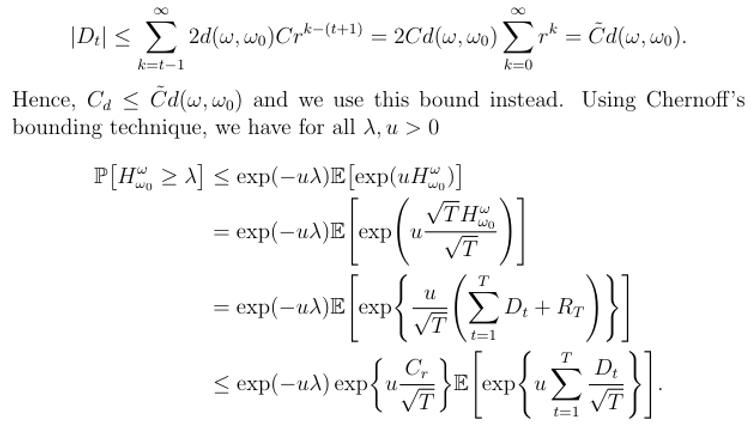


Appendix B.1. Uniform convergence of LT



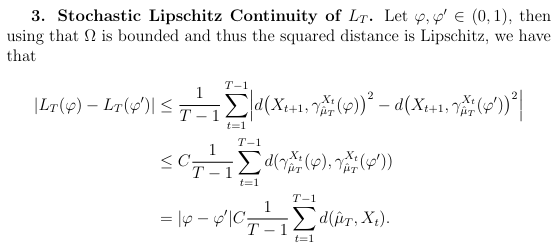
Again using that Ω is bounded, the average is also bounded and we obtain the desired result.
Reference
Armantier, O., Topa, G., Van der Klaauw, W., Zafar, B., 2017. An overview of the survey of consumer expectations. Economic Policy Review , 51–72.
Baˇc´ak, M., 2014. Computing Medians and Means in Hadamard Spaces. SIAM Journal on Optimization 24, 1542–1566. URL: https://epubs.siam.org/ doi/abs/10.1137/140953393, doi:10.1137/140953393. publisher: Society for Industrial and Applied Mathematics
van den Boogaart, K.G., Egozcue, J.J., Pawlowsky-Glahn, V., 2014. Bayes Hilbert Spaces. Australian & New Zealand Journal of Statistics 56, 171–194. URL: https://onlinelibrary.wiley.com/doi/10.1111/ anzs.12074, doi:10.1111/anzs.12074.
Bosq, D., 2000. Linear Processes in Function Spaces. volume 149 of Lecture Notes in Statistics. Springer New York, New York, NY. URL: http://link.springer.com/10.1007/978-1-4612-1154-9, doi:10.1007/978-1-4612-1154-9.
Bult´e, M., Sørensen, H., 2023. Medoid splits for efficient random forests in metric spaces. URL: http://arxiv.org/abs/2306.17031, doi:10.48550/ arXiv.2306.17031. arXiv:2306.17031 [stat].
Burago, D., Burago, Y., Ivanov, S., 2001. A Course in Metric Geometry. volume 33 of Graduate Studies in Mathematics. American Mathematical Society, Providence, Rhode Island. URL: http://www.ams.org/gsm/033, doi:10.1090/gsm/033.
Caner, M., 2006. M-estimators with non-standard rates of convergence and weakly dependent data. Journal of Statistical Planning and Inference 136, 1207–1219. URL: https://linkinghub.elsevier.com/retrieve/pii/ S0378375804003647, doi:10.1016/j.jspi.2004.09.004.
Caponera, A., Marinucci, D., 2021. Asymptotics for spherical functional autoregressions. The Annals of Statistics 49. URL: https://projecteuclid.org/ journals/annals-of-statistics/volume-49/issue-1/ Asymptotics-for-spherical-functional-autoregressions/10. 1214/20-AOS1959.full, doi:10.1214/20-AOS1959.
Chen, Y., Lin, Z., M¨uller, H.G., 2021. Wasserstein Regression. Journal of the American Statistical Association , 1–14URL: https://www. tandfonline.com/doi/full/10.1080/01621459.2021.1956937, doi:10. 1080/01621459.2021.1956937.
Dietrich, A.M., Kuester, K., M¨uller, G.J., Schoenle, R., 2022. News and uncertainty about COVID-19: Survey evidence and short-run economic impact. Journal of Monetary Economics 129, S35–S51. URL: https:// linkinghub.elsevier.com/retrieve/pii/S0304393222000216, doi:10. 1016/j.jmoneco.2022.02.004.
Dubey, P., M¨uller, H.G., 2019. Fr´echet analysis of variance for random objects. Biometrika 106, 803–821. URL: https://academic.oup.com/ biomet/article/106/4/803/5609104, doi:10.1093/biomet/asz052.
Dubey, P., M¨uller, H.G., 2020. Fr´echet change-point detection. The Annals of Statistics 48, 3312–3335. URL: https://projecteuclid. org/journals/annals-of-statistics/volume-48/issue-6/Fr% c3%a9chet-change-point-detection/10.1214/19-AOS1930.full, doi:10.1214/19-AOS1930. publisher: Institute of Mathematical Statistics.
Fréchet, M., 1948. Les ´el´ements al´eatoires de nature quelconque dans un espace distanci´e, in: Annales de l’institut Henri Poincar´e, pp. 215–310. Issue: 4.
Ghodrati, L., Panaretos, V.M., 2023. On Distributional Autoregression and Iterated Transportation. URL: http://arxiv.org/abs/2303.09469, doi:10.48550/arXiv.2303.09469. arXiv:2303.09469 [stat].
Hanneke, S., Kontorovich, A., Sabato, S., Weiss, R., 2021. Universal Bayes consistency in metric spaces. The Annals of Statistics 49, 2129–2150. URL: https://projecteuclid. org/journals/annals-of-statistics/volume-49/issue-4/ Universal-Bayes-consistency-in-metric-spaces/10.1214/ 20-AOS2029.full, doi:10.1214/20-AOS2029. publisher: Institute of Mathematical Statistics.
Hemerik, J., Goeman, J., 2018. Exact testing with random permutations. TEST 27, 811–825. URL: https://doi.org/10.1007/ s11749-017-0571-1, doi:10.1007/s11749-017-0571-1.
Hoeffding, W., Robbins, H., 1948. The central limit theorem for dependent random variables. Duke Mathematical Journal 15, 773–780. URL: https://projecteuclid.org/ journals/duke-mathematical-journal/volume-15/issue-3/ The-central-limit-theorem-for-dependent-random-variables/ 10.1215/S0012-7094-48-01568-3.full, doi:10.1215/ S0012-7094-48-01568-3. publisher: Duke University Press.
Jiang, F., Gao, H., Shao, X., 2023. Testing serial independence of objectvalued time series. Biometrika , asad069URL: https://doi.org/10. 1093/biomet/asad069, doi:10.1093/biomet/asad069.
K¨ostenberger, G., Stark, T., 2023. Robust Signal Recovery in Hadamard Spaces. URL: http://arxiv.org/abs/2307.06057, doi:10.48550/ arXiv.2307.06057. arXiv:2307.06057 [math, stat].
Lin, Z., 2019. Riemannian Geometry of Symmetric Positive Definite Matrices via Cholesky Decomposition. SIAM Journal on Matrix Analysis and Applications 40, 1353–1370. URL: https://epubs.siam.org/doi/ abs/10.1137/18M1221084, doi:10.1137/18M1221084. publisher: Society for Industrial and Applied Mathematics.
Mazzuco, S., Scarpa, B., 2015. Fitting Age-Specific Fertility Rates by a Flexible Generalized Skew Normal Probability Density Function. Journal of the Royal Statistical Society Series A: Statistics in Society 178, 187– 203. URL: https://doi.org/10.1111/rssa.12053, doi:10.1111/rssa. 12053.
McCormack, A., Hoff, P., 2022. The Stein effect for Fr´echet means. The Annals of Statistics 50, 3647–3676. URL: https: //projecteuclid.org/journals/annals-of-statistics/volume-50/ issue-6/The-Stein-effect-for-Fr%c3%a9chet-means/10.1214/ 22-AOS2245.full, doi:10.1214/22-AOS2245. publisher: Institute of Mathematical Statistics.
McCormack, A., Hoff, P.D., 2023. Equivariant estimation of Fr´echet means. Biometrika , asad014URL: https://doi.org/10.1093/biomet/asad014, doi:10.1093/biomet/asad014.
Meeks, R., Monti, F., 2023. Heterogeneous beliefs and the Phillips curve. Journal of Monetary Economics URL: https://www. sciencedirect.com/science/article/pii/S0304393223000703, doi:10.1016/j.jmoneco.2023.06.003.
Newey, W.K., 1991. Uniform Convergence in Probability and Stochastic Equicontinuity. Econometrica 59, 1161. URL: https://www.jstor.org/ stable/2938179?origin=crossref, doi:10.2307/2938179.
Panaretos, V.M., Zemel, Y., 2016. Amplitude and phase variation of point processes. The Annals of Statistics 44. URL: https: //projecteuclid.org/journals/annals-of-statistics/volume-44/ issue-2/Amplitude-and-phase-variation-of-point-processes/10. 1214/15-AOS1387.full, doi:10.1214/15-AOS1387.
Panaretos, V.M., Zemel, Y., 2020. An Invitation to Statistics in Wasserstein Space. SpringerBriefs in Probability and Mathematical Statistics, Springer International Publishing, Cham. URL: http://link.springer.com/10. 1007/978-3-030-38438-8, doi:10.1007/978-3-030-38438-8.
Petersen, A., Muller, H.G., 2019. Frechet regression for random objects with Euclidean predictors , 29.
Petersen, A., M¨uller, H.G., 2016. Functional data analysis for density functions by transformation to a Hilbert space. The Annals of Statistics 44. URL: http://arxiv.org/abs/1601.02869, doi:10.1214/ 15-AOS1363. arXiv: 1601.02869.
Petersen, A., Zhang, C., Kokoszka, P., 2022. Modeling Probability Density Functions as Data Objects. Econometrics and Statistics 21, 159–178. URL: https://linkinghub.elsevier.com/retrieve/pii/ S245230622100054X, doi:10.1016/j.ecosta.2021.04.004.
Raginsky, M., Sason, I., 2013. Concentration of Measure Inequalities in Information Theory, Communications, and Coding. Foundations and Trends® in Communications and Information Theory 10, 1–246. URL: https://www.nowpublishers.com/article/Details/CIT-064, doi:10. 1561/0100000064. publisher: Now Publishers, Inc.
Ramsay, J.O., Silverman, B.W., 2005. Functional data analysis. Springer series in statistics. 2nd ed ed., Springer, New York.
Scott, D.W., 1992. Multivariate Density Estimation: Theory, Practice, and Visualization. Wiley. URL: http://dx.doi.org/10.1002/ 9780470316849, doi:10.1002/9780470316849. iSSN: 1940-6347 Publication Title: Wiley Series in Probability and Statistics.
Srivastava, A., Klassen, E.P., 2016. Functional and Shape Data Analysis. Springer Series in Statistics, Springer New York, New York, NY. URL: http://link.springer.com/10.1007/978-1-4939-4020-2, doi:10.1007/978-1-4939-4020-2.
Sturm, K.T., 2003. Probability measures on metric spaces of nonpositive curvature, in: Auscher, P., Coulhon, T., Grigor’yan, A. (Eds.), Contemporary Mathematics. American Mathematical Society, Providence, Rhode Island. volume 338, pp. 357–390. URL: http://www.ams.org/conm/338/, doi:10.1090/conm/338/06080.
van der Vaart, A.W., Wellner, J.A., 1996. Weak Convergence and Empirical Processes. Springer Series in Statistics, Springer New York, New York, NY. URL: http://link.springer.com/10.1007/978-1-4757-2545-2, doi:10.1007/978-1-4757-2545-2.
Wu, W.B., Shao, X., 2004. Limit theorems for iterated random functions. Journal of Applied Probability 41, 425–436. URL: https://www.cambridge.org/core/journals/journal-of-applied-probability/ article/abs/limit-theorems-for-iterated-random-functions/ 9CA522B1DE090C02B7374ED8212739AB#, doi:10.1239/jap/1082999076. publisher: Cambridge University Press.
Xavier, J., Manton, J., 2006. On the Generalization of AR Processes To Riemannian Manifolds, in: 2006 IEEE International Conference on Acoustics Speed and Signal Processing Proceedings, IEEE, Toulouse, France. pp. V–1005–V–1008. URL: http://ieeexplore.ieee.org/document/ 1661448/, doi:10.1109/ICASSP.2006.1661448.
Yoshiyuki, A., 2017. A Functional Linear Regression Model in the Space of Probability Density Functions. Discussion papers URL: https://ideas. repec.org//p/eti/dpaper/17015.html. number: 17015 Publisher: Research Institute of Economy, Trade and Industry (RIETI).
Zhu, C., M¨uller, H.G., 2021. Autoregressive Optimal Transport Models. URL: http://arxiv.org/abs/2105.05439. arXiv:2105.05439 [stat].
Zhu, C., M¨uller, H.G., 2022. Spherical Autoregressive Models, With Application to Distributional and Compositional Time Series. URL: http: //arxiv.org/abs/2203.12783. arXiv:2203.12783 [stat].
Authors:
(1) Matthieu Bult´e, Department of Mathematical Sciences, University of Copenhagen, and Faculty of Business Administration and Economics, Bielefeld University;
(2) Helle Sørensen, Department of Mathematical Sciences, University of Copenhagen.
This paper is

