Table of Links
3. The GAR(1) Model
3.1. Model and Stationary Solution
4. Estimation of model parameters and 4.1. Fréchet mean
5. Testing for the absence of serial dependence
6.1. R with multiplicative noise
6.2. Univariate distributions with a density
Appendix A. General results in Hadamard spaces
2. Preliminaries

While the existence of the variance in standard spaces implies the existence of a mean, this is not necessarily the case in general metric spaces. Furthermore, on its own, a metric space offers very little to define parametric models. We now present the additional structure that will be used in this work to construct models for time series of random objects following the presentation in Burago et al. (2001) and Sturm (2003).

Hadamard spaces can also be defined via comparison triangles. This approach is not described here, see Chapter 4 of Burago et al. (2001) for such a presentation of Hadamard spaces. The following proposition from Sturm (2003) shows that Hadamard spaces are geodesic spaces, and that (2) holds along geodesics.

We mention some further useful results in Appendix A and refer the reader to Sturm (2003) for a thorough review of the subject.
We now present a few examples from Sturm (2003) of Hadamard spaces and ways of building Hadamard spaces out of existing ones. The most wellknown case of Hadamard space are Hilbert spaces. This allows to approach Functional Data Analysis (see Ramsay and Silverman (2005)) tasks from a random object perspective.

Hilbert spaces are examples of flat spaces in which the NPC inequality holds to equality. Manifolds of negative sectional curvature also are Hadamard spaces.
Example 2.3 (Constructed Spaces). Let (Ω, d) be a Hadamard space, then

One specific example of Hadamard spaces of particular interest is the space of one-dimensional density functions over R equipped with the 2- Wasserstein distance.

Another useful example of a constructed Hadamard space is that of symmetric positive definite (SPD) matrices together with the Log-Cholesky distance.

As a case of Example 2.3, this is a Hadamard space, which is also shown in Lin (2019), together with other properties of this space.
3. The GAR(1) Model
3.1. Model and Stationary Solution

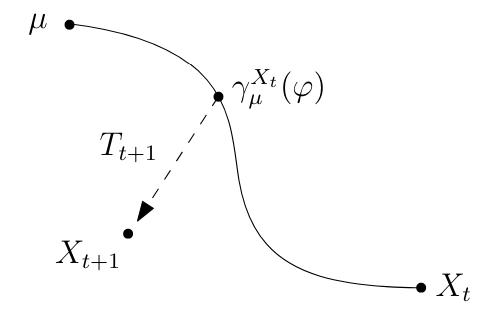

Unfortunately, this condition does not hold in every Hadamard space. Thus, we will assume the following.
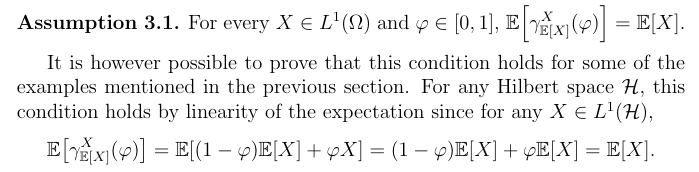
Furthermore, if the condition holds for a Hadamard space (Ω, d), then it also holds for a Hadamard space constructed by taking the image of a bijection ω as described in the second part of Example 2.3.


3.2. Identifability
Under the conditions of Theorem 3.3, Equation (5) has a stationary solution and the model features two quantities of interest: the time-invariant Fréchet mean of the time series µ ∈ Ω, and the concentration parameter φ ∈ [0, 1]. Before considering the estimation of these quantities, we show that both are identifiable. The identifiability of the Fréchet mean follows directly from the stationarity of the time series and the definition and existence of the Fréchet mean in a Hadamard space.


Authors:
(1) Matthieu Bult´e, Department of Mathematical Sciences, University of Copenhagen, and Faculty of Business Administration and Economics, Bielefeld University;
(2) Helle Sørensen, Department of Mathematical Sciences, University of Copenhagen.
This paper is

